La famiglia della distribuzioni di probabilità normali ha un'importante proprietà che la rende utilizzabile in un ampio raggio di applicazioni: questa proprietà è il teorema centrale limite e riguarda la distribuzione della somma o della media aritmetica di un campione scelto a caso di osservazioni. Siccome media aritmetica e somma dei dati differiscono tra loro per una costante moltiplicativa, d'ora in poi quello che si dirà riferito alla media aritmetica varrà sostanzialmente anche per la somma, fatti salvi alcuni aggiustamenti di costanti moltiplicative.
La formula che segue esprime quella che d'ora in avanti definiremo "media campionaria".
![]()
Capita spesso di trovarsi di fronte a somme o medie artimetiche: ad es., le vendite mensili di un'azienda consistono nella somma delle vendite dei singoli rappresentanti.
Il teorema centrale limite afferma che, in condizioni abbastanza generali, somme e medie di misurazioni casuali ricavate da una popolazione tendono a possedere approssimativamente una distribuzione a forma di campana, nel senso che si spiegherà in seguito.
La rilevanza di questo concetto è forse meglio comprensibile se ci si avvale di un esempio. Quest'esempio è un'applicazione del metodo di montecarlo, un metodo di campionamento simulato, nel quale si simula la situazione nella quale si vuole calcolare la probabilità di un certo evento.
Si consideri una popolazione di lanci di dadi, generata lanciando un dado un'infinitamente grande numero di volte, con distribuzione di probabilità data dalla seguente immagine:
Si estragga un campione di n = 5 misurazioni dalla popolazione lanciando cinque volte un dado e si prenda nota delle cinque osservazioni, come indicato nella seguente tabella:
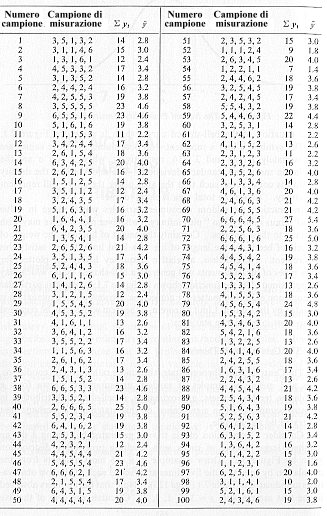
Si noti che i numeri osservati nel primo campione erano y = (3, 5, 1, 3, 2). Si calcoli la somma delle
cinque misurazioni e la media campionaria, ![]() .
Per scopi sperimentali, si ripeta la procedura di campionatura un centinaio di volte, o, preferibilmente,
un numero maggiore di volte. Si costruisca ora un istogramma della frequenza per
.
Per scopi sperimentali, si ripeta la procedura di campionatura un centinaio di volte, o, preferibilmente,
un numero maggiore di volte. Si costruisca ora un istogramma della frequenza per
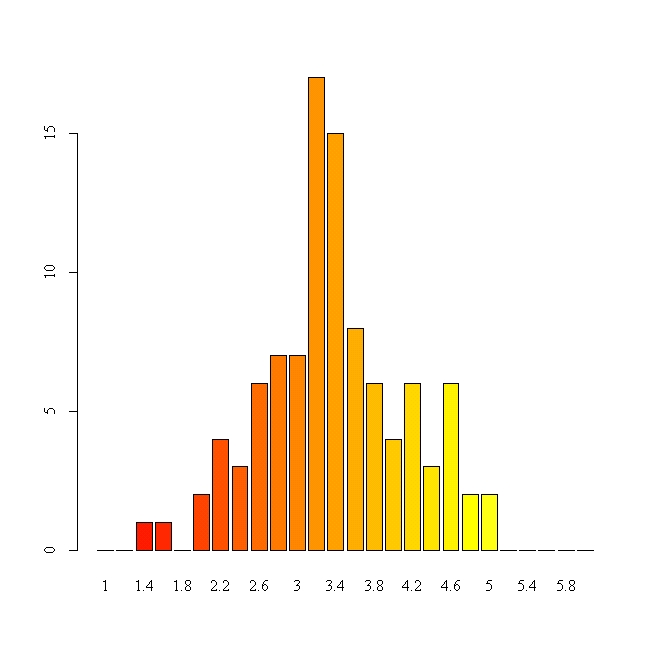
![]() per i cento campioni e si osservi la distribuzione
risultante nella prima immagine.
per i cento campioni e si osservi la distribuzione
risultante nella prima immagine.
Compare un risultato interessante: benché i valori di y nella popolazione (Y = {1, 2, 3, 4, 5, 6}) siano equiprobabili e perciò posseggano una distribuzione di probabilità che è perfettamente orizzontale, la distribuzione delle medie campionarie scelta dalla popolazione possiede una distribuzione con un addensamento al centro e una densità minore sulle code a sinistra e a destra. Inoltre, si osserva che, se si ripete l'esperimento delineato in precedenza per un campione più grande (es.: n = 10), si noterà che la distribuzione delle medie campionarie tende ad avvicinarsi sempre più alla forma di una campana, via via che n cresce.
Pertanto, il teorema centrale limite, che si riferisce a "qualunque" popolazione da cui si
estraggano dei campioni, dice che:
Il teorema centrale limite è importante innanzitutto perché spiega il motivo per cui alcune misurazioni tendono a possedere approssimativamente una distribuzione normale. Si può immaginare l'altezza umana come composta da un numero di elementi - ognuno dei quali casuale - associati con variabili come l'altezza della madre e del padre, l'ambiente, la dieta, ecc. Se ognuno di questi elementi tende ad aggiungersi agli altri per fornire la misurazione dell'altezza, allora l'altezza è la "somma" di un numero di variabili casuali e il teorema centrale limite può essere applicato e fornire una distribuzione delle altezze che è approssimativamente normale.
In secondo luogo, l'altro e più importante contributo del teorema centrale limite si esplica nell'inferenza statistica, perché molte procedure statistiche di verifica di ipotesi fanno uso di questo teorema.
Ritorna alla pagina principale.
Ritorna alla homepage di Lorenzo Azzalini.